Let
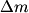 be the change in the mass of the rocket during a small time interval be the change in the mass of the rocket during a small time interval 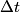 . So, . So, 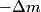 is the mass of the exhaust released from the rocket during the time interval is the mass of the exhaust released from the rocket during the time interval 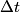 . Let . Let  be the velocity of the rocket before the mass be the velocity of the rocket before the mass 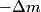 is released, is released, 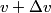 be the velocity of the rocket after the mass be the velocity of the rocket after the mass 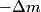 is released, and is released, and 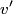 be the velocity of the mass be the velocity of the mass 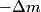 after it is released. Conservation of momentum tells us that after it is released. Conservation of momentum tells us that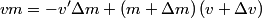 Ignoring the second order term 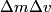 gives gives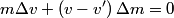 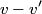 is the speed of the exhaust relative to the rocket, so answer (E) is correct. is the speed of the exhaust relative to the rocket, so answer (E) is correct. |